Measuring Cooperation and Reciprocity

From Evolution and Games

Jump to: navigation, search

Here we formally define measures for cooperation and reciprocity.

Contents

Introduction

There are two reasons why we would like to have measures for cooperativeness and reciprocity. The first and most important reason is obvious; we would simply like to know how cooperative, and how reciprocal, strategies are during a run. The second reason is that these measures may serve as an indication of indirect invasions. Typically an indirect invasion is characterized by a change in reciprocity followed by a change in cooperativeness.

Measuring cooperation

Any measure of cooperativeness will have to weigh the different histories, and as we will see, every choice how to weigh them has appealing properties and drawbacks. In contrast to the definitions earlier, here it is more natural to look at histories that only reflect what actions the other player has played. This captures all relevant histories for the measurement of cooperativeness, because what a strategy S itself has played is uniquely determined by the history of actions by the other player.

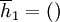
\overline{h}_{1}=()

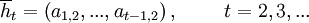
\overline{h}_{t}=\left( a_{1,2},...,a_{t-1,2}\right) ,\qquad ~t=2,3,...


Again, we will sometimes also write 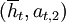(\overline{h}_{t},a_{t,2}) for a history 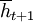\overline{h}_{t+1}, and we get the following sets of possible histories at time t.

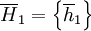
\overline{H}_{1}=\left\{ \overline{h}_{1}\right\}

\overline{H}_{t}=\prod_{i=1}^{t-1}A\qquad \qquad t=2,3,...


With the repeated prisonners dilemma we have A = C,D, so in that case there are 2t − 1 histories 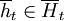\overline{h}_{t} \in \overline{H}_{t}

We begin with a measure that tells us how cooperative a strategy is, given that it is facing a history 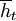\overline{h}_{t}. 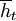If we weigh a history at time t + s with the probability that the game actually reaches round t + s − 1, given that it has already reached round t − 1, and if we also divide by the number of different histories of length t + s − 1, under the restriction that the first t − 1 rounds of these histories are given by \overline{h}_{t}, we get the following. Note that this measure does not depend on the environment a strategy is in.


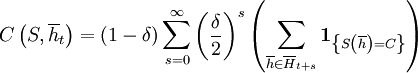
C\left( S,\overline{h}_{t}\right) =\left( 1-\delta \right) \sum_{s=0}^{\infty }\left( \frac{\delta }{2}\right) ^{s}\left( \sum_{\overline{h}\in \overline{H}_{t+s}}\mathbf{1}_{\left\{ S\left( \overline{h}\right) =C\right\} }\right)

The overall cooperativeness of a strategy S can then be defined as the cooperativeness at the beginning, where we have the empty history; 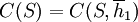C(S) =C(S,\overline{h}_{1}).

Graphic interpretation

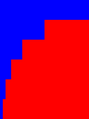
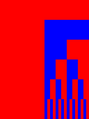
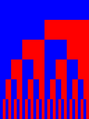
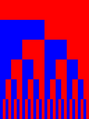
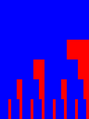
An intuition for what this measure does can be gained from the following figure. The top bar represents the empty history. The second bar represents histories of length 1, and is split in two; the history where the other has cooperated, and the one where the other has defected. The third bar represents histories of lenth 2, and is split in four; the histories CC, CD, DC and DD. This continues indefinitely, but for the pictures we restrict ourselves to histories of length 5 or less. If a part is blue, then that means that the strategy reacts to this history with cooperation, if it is red, then the strategy reacts with defection. Cooperativeness weighs the blueness of those pictures.

Always Cooperate

Always Defect

Condition on first move

Grim Trigger

Negative Handshake (DTFT)

Tit for Tat

Tat for Tit

Tit for two Tats

Win stay lose shift

Measure of cooperation for well-known strategies

It is obvious that C(AllC) = 1 and that C(AllD) = 0. A strategy that starts with cooperation, and further conditions play on the first move entirely has cooperativeness 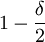1-\frac{\delta }{2}. This is sensible; if δ = 0, then the first move is the only move, and since this strategy cooperates on the first move, it should have cooperativeness measure 1. On the other hand, except for the first move, this strategy cooperates in exactly half of the histories of length t for all t > 1. Therefore it makes sense that if δ goes to 1, then cooperativeness goes to \frac{1}{2}.

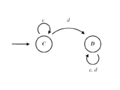
For tit for tat, we have:

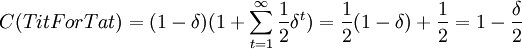
C(TitForTat) =( 1-\delta) ( 1+\sum_{t=1}^{\infty }\frac{1}{2}\delta ^{t}) =\frac{1}{2}( 1-\delta) +\frac{1}{2} = 1-\frac{\delta }{2}

More simple computations show that:

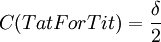C(TatForTit) =\frac{\delta }{2}, and

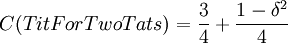C(TitForTwoTats)=\frac{3}{4}+\frac{1-\delta ^{2}}{4}.

The last simple computation shows that

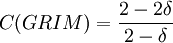C(GRIM) =\frac{2-2\delta }{2-\delta },

which is 1 at δ = 0 for similar reasons, and goes to 0 if δ goes to 1.

Measuring reciprocity

A measure for reciprocity can be constructed by comparing how much the cooperativeness of strategy S is changed if its opponent plays D rather than C. Again, histories of the same length are weighted equally here.

R(S) =\sum_{t=1}^{\infty} \sum_{\overline{h}\in \overline{H}_{t}} (\frac{\delta }{2}) ^{t-1} [ C(S,(\overline{h},C)) -C(S,(\overline{h},D))]

In the figure above, this is visualized as the difference in blueness below two neighbouring bits that share their history up to the one before last period.

Measure of reciprocity for well-known strategies

Simple calculations now give that R(AllC) = R(AllD) = 0 and R(TFT) = 1. Also, if we look at a strategy that only conditions on the first move and that defects forever if the first move of the other was D, and cooperates forever if the first move of the other was C, this strategy also has reciprocity 1. It is not hard to see that − 1 and + 1 are in fact the lower and upper bounds for reciprocity with this equal weighing of all strategies of the same length.

Likewise,

R(GRIM) =\sum_{t=1}^{\infty }(\frac{\delta }{2}) ^{t-1}[ \frac{2-2\delta }{2-\delta }-0] =\frac{4(1-\delta) }{(2-\delta) ^{2}} =\frac{4( 1-\delta) }{( 2-\delta) ^{2}}.

R(TFT)=\sum_{t=1}^{\infty} \sum ( \frac{\delta }{2}) ^{t-1} [\frac{1}{2}+\frac{1}{2}( 1-\delta) -( \frac{1}{2}-\frac{1}{2}( 1-\delta) )] 2^{t-1}=\sum_{t=1}^{\infty }\delta ^{t-1}(1-\delta) =1


Note that here the reciprocity of Grim Trigger is lower than that of TFT, which is due to the fact that for many histories GRIM will only play a sequence of D's either way.

Density-dependent measures

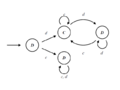
Alternatively we could measure the cooperativeness and reciprocity of a strategy given the population it is in. In that case, we should not weight all histories of a given length equally, but in the proportions in which they do occur given the actual population of strategies. Hence the weight (1 / 2)t − 1, which is one divided by the number of strategies in Ht, will then be replaced by their actual proportions. For instance, in a population that consists of any mixture of AllC, TFT and GRIM, the only history at time t that occurs, is a sequences of t − 1 consecutive C's. The measure for cooperativeness then simply becomes the expected times a strategy plays C divided by the expected number of rounds.

Suppose the population is given by a vector of frequencies x = [x1,...,xN] where xi is the frequency of strategy Si. Then we define the population-dependent cooperativeness of a strategy S as follows:

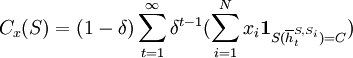
C_{x}(S) =( 1-\delta) \sum_{t=1}^{\infty}\delta ^{t-1}(\sum_{i=1}^{N}x_{i}\mathbf{1}_{{ S(\overline{h}_{t}^{S,S_{i}}) =C}})

In a population with only AllC, TFT and GRIM, cooperativeness of all these three strategies is 1. In an infinitely large population of αTFT and (1 − α)AllD, cooperativeness of TFT is 1 − δ + δα .

A reasonable way of measuring reciprocity is to compare actual histories with histories that would have unfolded after one-step deviations. So let 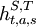h_{t,a,s}^{S,T} be the history that for the first t − 1 steps unfolds recurcively between strategy S and T - as above;

h_{1}^{S,T}=()

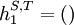
and the recursion step

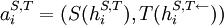
a_{i}^{S,T}=(S(h_{i}^{S,T}) ,T(h_{i}^{S,T\leftarrow}))

h_{i+1}^{S,T}=( h_{i},a_{i}^{S,T}) ,\qquad ~\qquad \qquad \qquad \qquad i=1,2,...,t-1.

Only at time t the opponent plays a, while strategy S does not deviate and plays 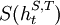S(h_{t}^{S,T});

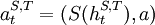
a_{t}^{S,T}=(S( h_{t}^{S,T}) ,a)

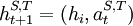h_{t+1}^{S,T}=( h_{i},a_{t}^{S,T}).

After that we go back to the normal recursion step

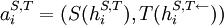
a_{i}^{S,T}=(S( h_{i}^{S,T}) ,T(h_{i}^{S,T\leftarrow}))

h_{i+1}^{S,T}=(h_{i},a_{i}^{S,T}) ,\qquad ~\qquad \qquad \qquad \qquad i=t+1,...t+s

If 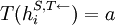T(h_{i}^{S,T\leftarrow }) =a, then this is 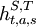h_{t,a,s}^{S,T} is just the actual history 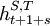h_{t+1+s}^{S,T}, but if 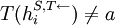T(h_{i}^{S,T\leftarrow }) \neq a, it is a counterfactual history after a one-step deviation. The history 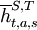\overline{h}_{t,a,s}^{S,T}, as above, just gives the actions of player T and ignores those of player S.

With this definition, we can make a measure for reciprocity as follows:

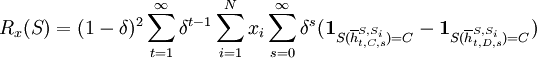
R_{x}(S) =(1-\delta)^{2} \sum_{t=1}^{\infty }\delta^{t-1}\sum_{i=1}^{N}x_{i}\sum_{s=0}^{\infty}\delta^{s}(\mathbf{1}_{{S(\overline{h}_{t,C,s}^{S,S_{i}}) =C} }-\mathbf{1}_{{S(\overline{h}_{t,D,s}^{S,S_{i}}) =C}})


In a population of GRIM only, it is relatively easy to see that the reciprocity of GRIM is 1; the path of play between GRIM and itself is just a sequence of C's, while after a deviation GRIM just plays a sequence of D's. So at any time t, the discounted difference between these sequence from then on, normalised by multiplying by one of the t(1 − δ)'s, is 1. So discounting over t and normalizing by the other (1 − δ) gives a reciprocity measure of 1.

In a population of TFT only, the reciprocity of TFT is 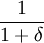\frac{1}{1+\delta }. Again, the path of play between TFT and itself is a sequence of C's, but now, on the path after any deviation, TFT plays a sequence of alternating D's and C's. So at any time t, the discounted and normalized difference between them is 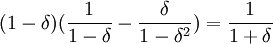(1-\delta) ( \frac{1}{1-\delta }-\frac{\delta }{1-\delta ^{2}}) =\frac{1}{1+\delta }. So discounting over t and normalizing by the other (1 − δ) gives the same number.

This comparison is in line with what we might want from a reciprocity measure that depends on the actual population; at any stage, the threat that grim trigger poses to itself is maximal, and larger than the threat TFT poses to itself.

Another comparison shows that this measure also picks up the fact that, if the punishment in Grim Trigger is in fact triggered on the path of play, then on the remainder of the path, GRIM is actually not reciprocal at all anymore. With TFT on the other hand, reciprocity actually remains the same, whether the punishment has been triggered in the past or not. This is reflected in the following example.

In a population of αTitForTat and (1 − α)TatForTit, the reciprocity of TitForTat is 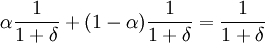\alpha \frac{1}{1+\delta }+( 1-\alpha) \frac{1}{1+\delta }=\frac{1}{1+\delta }; the reciprocity of TitForTat against itself was computed above, and for the computation of TitForTat against TatForTit it is enough to realize that the comparison between actual and counterfactual is between DCDC... versus CCCC... at odd t's and between CDCD... versus DDDD... at even t's.

In a population of αGRIM and (1 − α)TatForTit, the reciprocity of GRIM is α + (1 − α)(1 − δ) = 1 − δ + αδ; in the latter interaction, GRIM only alters its behaviour in response to a change at t = 1. So for not too large α - implying that there is enough TatForTit to have a noticeable effect of the punishment being triggered - and not too small δ GRIM now is actually less reciprocal than TitForTat.

Dependence on the population a strategy finds itself in can be seen as a good or a bad thing. For picking up indirect invasions, it seems to be a good thing; changes far off the current path of play between strategies do not change this reciprocity measure; it only changes if a strategy mutates into one that reacts differently to a one-step deviation. This implies that only becoming more or becoming less reciprocal in the way that is relevant for indirect invasions is picked up. On the other hand, it does not lend itself for a general, environment-independent statement of how reciprocal or cooperative a strategy is.


Another possibility is to only look at the actions directly after a one-step deviation. Then we would get

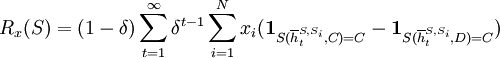
R_{x}(S) =(1-\delta) \sum_{t=1}^{\infty}\delta ^{t-1} \sum_{i=1}^{N}x_{i}(\mathbf{1}_{{S(\overline{h}_{t}^{S,S_{i}},C) =C} }-\mathbf{1}_{{ S(\overline{h}_{t}^{S,S_{i}},D) =C} })

Here the reciprocity of AllC is 0 again. The reciprocity of both TFT and GRIM in a population of TFT, GRIM and AllC is 1 here.

Retrieved from "http://www.evolutionandgames.nl/wiki/index.php?title=Measuring_Cooperation_and_Reciprocity"